Des points, des triangles et des pixels fantomes ?

J'ai pu grandement avancer depuis mon dernier post sur la camera de mon projet [Terminoux3D](https://github.com/Elowarp/3D-engine-C), notamment sur l'importation de fichiers .obj et les lumières. Cependant, mon moteur 3D souffre encore d'un problème qu'il est temps de régler : les pixels fantômes. _Dans cet article, nous utiliserons sans distinction les termes `pixels` et `caractères` compte tenu de la nature du projet._  _Figure : On voit ici, sur certaines faces, des caractères et même des lignes entières manquantes/fantômes._ ## Le rendu dans le terminal Avant de continuer, il est nécessaire de comprendre le fonctionnement du programme sur la transformation d'un triangle 3D jusqu'à l'affichage dans le terminal. ### Projection en 2D On commence par représenter le triangle 3D dans la base de la caméra (cf [article sur la caméra](https://www.elowarp.fr/blog/terminoux3d_rotation/)), pour ensuite pouvoir projeter les points dans le plan de la caméra (aka l'écran).  _Figure : Projection d'une pyramide sur un écran 2D, celui de la caméra._ Pour cela, on projette les points du triangle 3D dans le plan de la caméra en divisant les coordonnées x et z par la coordonnée y (la profondeur) du point. ```c vec2 coin = {v.x/v.y, v.z/v.y}; ``` On obtient alors un triangle 2D après l'avoir fait sur tous les coins. ### Conversion en pixels Ici la partie intéressante commence. Déjà, vu les configurations de terminaux infinies, il nous faut un moyen pour s'assurer d'avoir un carré affiché dans le terminal lorsque l'on veut un carré, et non un rectangle. On représente le plan de la caméra dans un carré de coordonnées entre -1 et 1. On va alors convertir ces coordonnées en coordonnées de caractères dans le terminal. Pour commencer, on va multiplier les coordonnées par le ratio hauteur/largeur du terminal et des caractères du terminal, nommé `ASPECT_RATIO_CHARACTER_SHELL` afin de s'assurer que le carré affiché dans le terminal soit un carré. ```c const float ASPECT_RATIO_CHARACTER_SHELL = 2.2; vec2 vec2_to_screen(float width, float width, vec2 v){ v.x = ASPECT_RATIO_CHARACTER_SHELL * (height/ width) * v.x + 1.0; v.y = -v.y + 1.0; ... return v; } ``` Un seul problème avec cette méthode est qu'on ne peut construire `ASPECT_RATIO_CHARACTER_SHELL` dans le programme. En effet, on ne peut pas récupérer en C les informations sur la police d'écriture utilisée par le terminal. Ainsi cette variable est un _magic number_ fonctionnant sur mon pc, mais qui ne fonctionnera pas sur un autre. Donc il se peut qu'en voulant faire le rendu d'un carré, le résultat final soit un rectangle chez vous. Bref, il ne reste plus qu'à convertir notre vecteur 2D (représentant un coin du triangle) en coordonnées de caractères dans le terminal. On va alors passer les coordonnées en coordonnées entre 0 et 1 (par les `+1.0` et `/2.0`) puis les multiplier par la largeur et la hauteur du terminal pour obtenir les coordonnées en pixels. ```c vec2 vec2_to_screen(float width, float width, vec2 v){ v.x = ASPECT_RATIO_CHARACTER_SHELL * (height / width) * v.x + 1.0; v.y = -v.y + 1.0; v.x = v.x * width / 2.0; v.y = v.y * height / 2.0; return v; } ``` _La division par 2 étant donné que nous représentons les coordonnées sur une distance de 2 (= 1 - (-1))._ On obtient alors les coordonnées en pixels du coin du triangle. Plus qu'à le faire sur tous les coins et dessiner le triangle. ### Dessin du triangle Pour dessiner le triangle, différentes approches sont possibles. Celle que j'ai choisie est de calculer un carré englobant le triangle, puis de parcourir tous les pixels de ce carré et de vérifier si le pixel est dans le triangle.  _Figure : En bleu, le carré englobant le triangle noir._ Pour cela, un simple calcul de minimum et de maximum des coordonnées des points du triangle suffit : ```c vec2 get_bottom_right_corner(triangle2D t){ vec2 br = {t.v1.x, t.v1.y}; if (t.v2.x > br.x) br.x = t.v2.x; if (t.v3.x > br.x) br.x = t.v3.x; if (t.v2.y > br.y) br.y = t.v2.y; if (t.v3.y > br.y) br.y = t.v3.y; return br; } ``` _On réalisera de même la fonction pour obtenir le coin en haut à gauche._ On va ensuite chercher à déterminer si un pixel est dans le triangle ou non. Pour cela, on va utiliser [la méthode](https://stackoverflow.com/questions/2049582/how-to-determine-if-a-point-is-in-a-2d-triangle) qui consiste à considérer chaque côté du triangle comme une droite et de vérifier si le pixel est à gauche (resp. en haut) ou à droite (resp. en bas) de chaque droite. En effet, si le pixel est à gauche (ou à droite) (resp. en haut ou en bas) de _chaque_ droite, alors il est dans le triangle. ```c // Calcule le signe de si le point est à gauche ou à droite de la droite float sign (vec2 v1, vec2 v2, vec2 v3){ return (v1.x - v3.x) * (v2.y - v3.y) - (v2.x - v3.x) * (v1.y - v3.y); } // Regarde si le retour de sign est le même pour les 3 côtés du triangle bool is_point_inside_triangle(triangle2D t, vec2 pos){ float d1, d2, d3; bool has_neg, has_pos; d1 = sign(pos, t.v1, t.v2); d2 = sign(pos, t.v2, t.v3); d3 = sign(pos, t.v3, t.v1); has_neg = (d1 <= 0) && (d2 <= 0) && (d3 <= 0); has_pos = (d1 >= 0) && (d2 >= 0) && (d3 >= 0); return has_neg || has_pos; } ```  _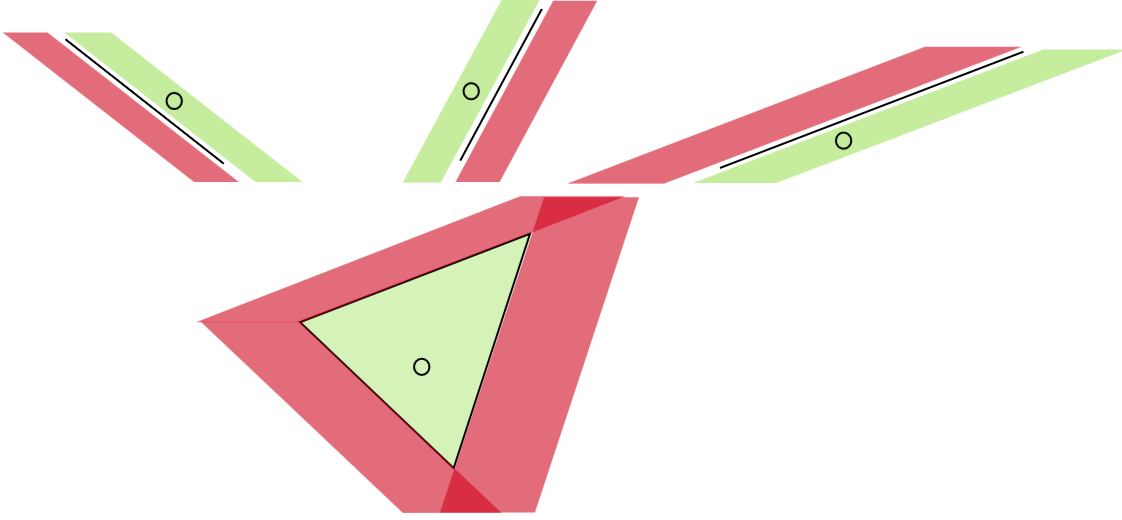Figure : Décomposition des 3 tests effectués sur la ligne du haut, et la conclusion en dessus, afin de savoir si un point est dans le triangle ou non._ On peut alors dessiner le triangle en parcourant tous les pixels du carré englobant et en vérifiant si le pixel est dans le triangle. ## Les pixels fantômes Alors comment diable y a-t-il des pixels manquants ? Je me suis cassé la tête sur ce problème pendant une dizaine d'heures, toujours tentant de nouvelles choses en vain. Ma première idée fut de me dire que étant donné un caractère, il a une certaine surface. Ainsi, il se pouvait que le calcul du point dans le triangle ne permettait pas de prendre en compte cette surface.  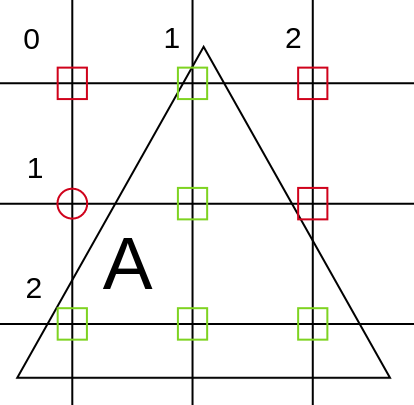_Figure : En rouge, les indices qui n'auront pas de caractère lors du rendu, en vert ceux qui en auront. On voit que pour le A, indice rond rouge, sa position n'est pas dans le triangle donc rien ne sera affiché alors qu'il serait plus logique d'afficher un caractère car celui ci est grandement recouvert par le triangle._ J'ai alors tenté de diviser chaque pixel en $decompo\_factor^2$ pixels plus petits, et de faire la moyenne de ces pixels pour savoir si le pixel devait être dessiné ou non. ```c void draw_triangle2D(char* pixels, triangle2D t, char c){ // Definition du carré englobant (br = bottom right, tl = top left) vec2 br = get_bottom_right_corner(t); vec2 tl = get_top_left_corner(t); vec2 dims = sub_vec2(br, tl); for(int i=0; i <= dims.y; i++){ for(int j=0; j <= dims.x; j++){ float sum = 0; // Crée les pixels internes qui seront utilisés pour savoir si le pixel // doit être dessiné // Ex : si decompo_factor = 2, les pixels internes seront // (0.25, 0.25) (0.75, 0.25) // (0.25, 0.75) (0.75, 0.75) // pour le pixel (0, 0) for(int k = 0; k < decompo_factor; k++){ for(int l = 0; l < decompo_factor; l++){ // Emplacement du pixel interne vec2 pixel = { tl.x+j+(float)l/decompo_factor + (float)1/decompo_factor, tl.y+i+(float)k/decompo_factor + (float)1/decompo_factor, }; if (is_point_inside_triangle(t, pixel)) sum += 1; } } // Emplacement du réel pixel vec2 pixelCoords = {tl.x+j, tl.y+i}; // Puis on fait la moyenne des pixels internes pour savoir // si le pixel doit être dessiné if (sum/(decompo_factor*decompo_factor) >= 0.5) change_pixel(pixels, pixelCoords, c); } } } ``` Mais **badaboum**, cela ne fonctionne absolument pas. Les pixels manquants sont toujours là (le paradoxe du pixel manquant présent ?). Bref je me suis alors dit que le problème venait de la fonction `is_point_inside_triangle` qui ne prenait pas en compte les cas limites tels que les coins et côtés du triangle. Cette piste fût assez vite écartée car les tests dans `tests.c` montraient que la fonction fonctionnait correctement sur ces cas là. J'ai même cherché à confirmer par différentes sources que la méthode de calcul d'un point dans un triangle était correcte. Mais alors, comment ? La réponse se cachent dans les fonctions données plus haut, c'est quelque chose de tout bête : _les arrondis_. Comment même imaginer qu'un problème si ridicule s'était glissé dans une des premières fonctions de tout le projet, remontant 4mois plus tôt ! En effet, les flottants n'étant pas des nombres exacts, les calculs de `tl` et `br` dans `get_bottom_right_corner` ne donnent pas toujours un carré englobant la totalité du triangle. Ainsi, lors du parcours des pixels de ce carré certains de ses bords ne sont pas pris en compte. D'où le simple ajout de `ceil` et `floor` qui ont permis de régler tous les problèmes : ```c vec2 get_bottom_right_corner(triangle2D t){ vec2 br = {t.v1.x, t.v1.y}; if (t.v2.x > br.x) br.x = t.v2.x; if (t.v3.x > br.x) br.x = t.v3.x; if (t.v2.y > br.y) br.y = t.v2.y; if (t.v3.y > br.y) br.y = t.v3.y; br.x = ceil(br.x); br.y = floor(br.y); return br; } ``` Et voilà, les pixels manquants sont bien partis. Comme quoi, pas besoin de monter dans les tours pour régler un pauvre problème de flottants :) *Ce ne sont pas des larmes que l'on peut voir sur mon visage non..*  _Figure : Un chat qui tourne en rond, sans problème d'affichage de caractères (avec, certes, un problème de compression)_