Moteur 3D + Terminal + ASCII = Terminoux3D

[Terminoux3D](https://github.com/Elowarp/3D-engine-C) est le petit nom que j'ai donné à mon dernier projet : Un moteur 3D dans le terminal, ou du moins une esquisse de moteur 3D écrite entièrement en C. Ce projet est en partie inspiré de la série de vidéos de [Quantale](https://www.youtube.com/watch?v=UkPTyojw7IA&list=PL9V1oyvT8aPwXSj-J3b2OQgcwP63u3f4R) où il implémente un moteur 3D du même genre mais sur Python. J'ai tout de même décidé d'y apporter ma touche personnelle, d'où ce post ! Le but affiché ici est de se mouvoir dans un environnement 3D directement dans le terminal : déplacement et rotation _via une caméra_ y compris ! Nous ne discuterons pas de toute l'implémentation ici mais seulement de comment la rotation dans l'espace et le rendu ont été implémentés. --- On commencera d'abord par comprendre comment est pensé le projet : On veut pouvoir avoir un environnement 3D avec un ensemble d'objets et pouvoir avoir une caméra déplaçable qui va les afficher dans le terminal, **on aura donc le point de vue de la caméra** (cet aspect est important pour la suite).  _Translation de la caméra dans l'espace_ Ainsi, comme dans les logiciels de 3D classique, nos objets seront représentés par une juxtaposition de triangles (d'où le triangle sur l'image). Chaque triangle est défini par ses trois sommets, ayant tous les trois, trois coordonnées. Ce qui justifie l'utilisation de ces types : ```C typedef struct { float x; float y; float z; } vec3; typedef struct { vec3 v1; vec3 v2; vec3 v3; } triangle3D; ``` De même, pour afficher des formes 3D en 2D sur un écran, et en particulier dans un terminal, il nous faut définir des triangles 2D définis par des points à 2 coordonnées, d'où des types similaires `vec2` et `triangle2D`. --- Concentrons nous maintenant sur la caméra et notamment la rotation dans l'espace. On associe à notre caméra une position et 3 vecteurs représentant une base, la base _orthonormée_ de notre caméra : ```C typedef struct { vec3 pos; vec3 v1; vec3 v2; vec3 v3; } camera; ``` Ainsi, à n'importe quel moment, on peut décrire les coordonnées d'un point dans la base canonique de $\mathbb{R^3}$ noté $B_c$ et dans la base de notre caméra, que l'on note $B_{cam}$.  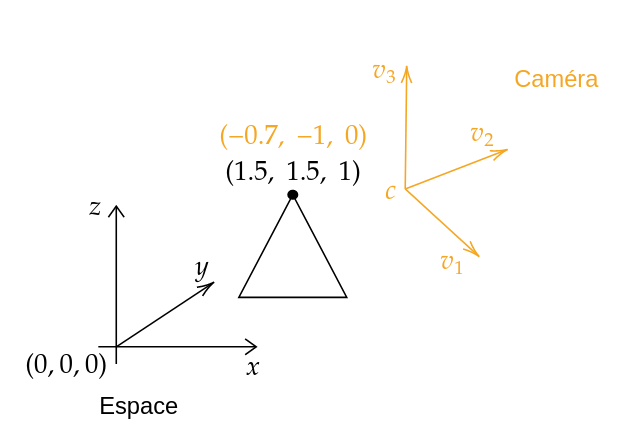_En noir le repère de l'espace, en orange le repère de la caméra d'origine $c$ et de base $(v_1, v_2, v_3)$. Les coordonnées du point du sommet du triangle écrite dans les deux bases selon les couleurs._ On notera que le vecteur $v_2$ est le vecteur normal au plan de la camera (formé des vecteurs $(v_1, v_3)$), selon lequel on projettera le triangle afin d'avoir une image 2D. On veut d'abord, avant de s'occuper du rendu, savoir comment faire tourner notre caméra. J'ai décidé d'utiliser les matrices de rotation en dimension 3 : $$ R_\theta = \begin{pmatrix} cos(\theta) & -sin(\theta) & 0\\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix} $$ _Ici écrite pour laisser invariant l'axe z, donc faire une rotation de gauche vers la droite ou inversement selon $\theta$._ Donc pour faire tourner notre caméra, on va faire tourner les vecteurs de notre base $B_{cam}$ par la relation suivante : $$ V' = R_\theta V $$ avec $V$ les coordonnées d'un des vecteurs de notre base caméra et $V'$ le vecteur tourné de $\theta$  _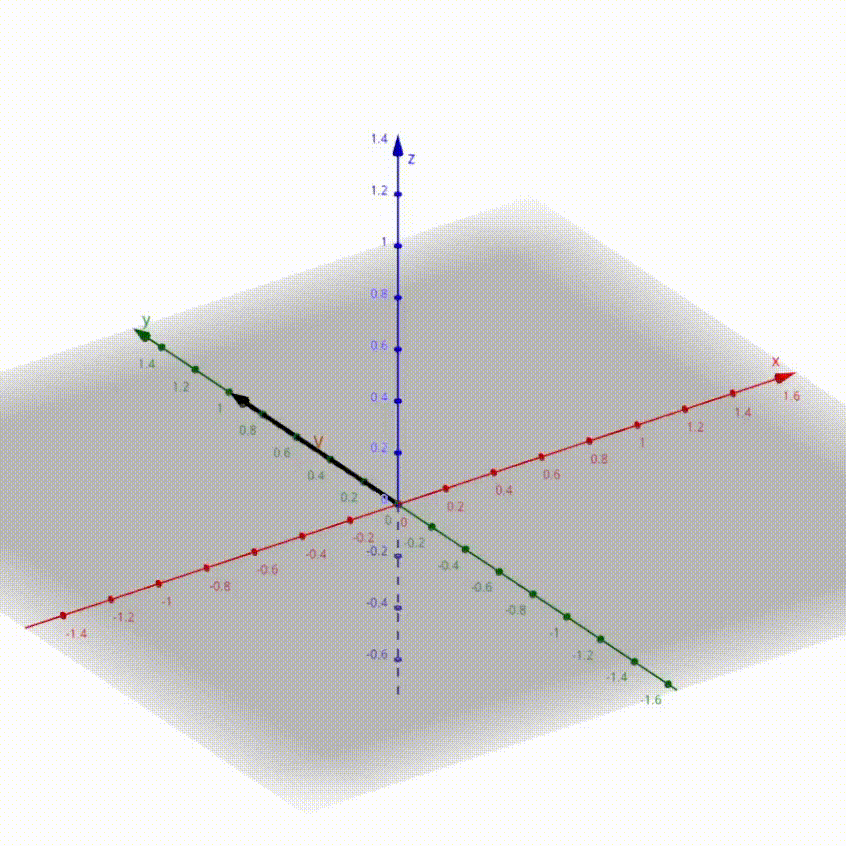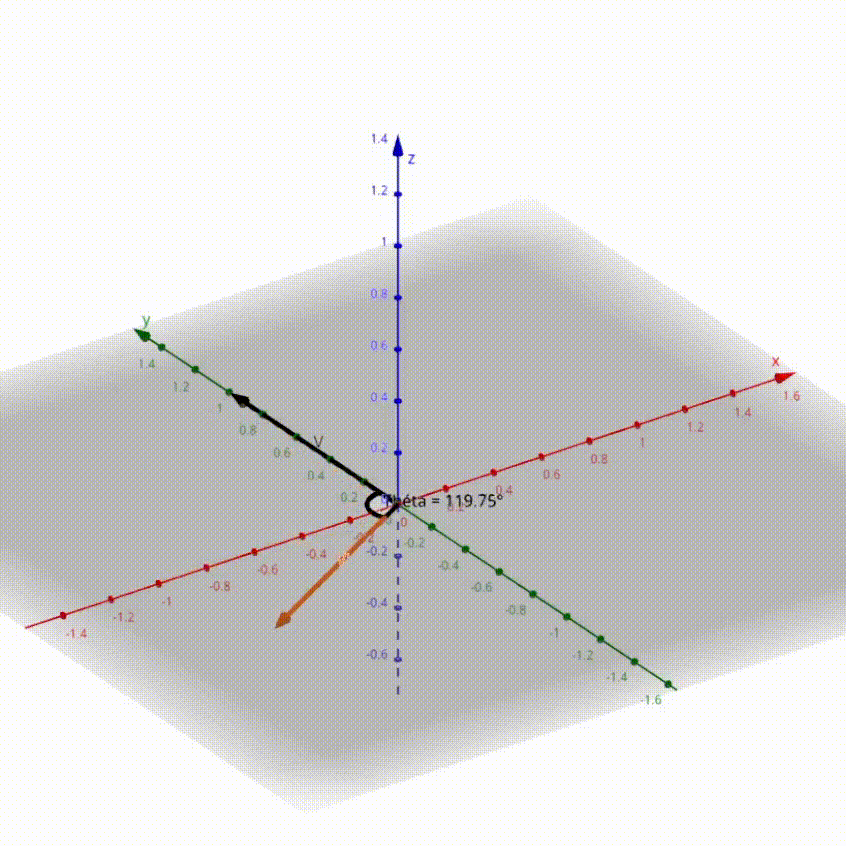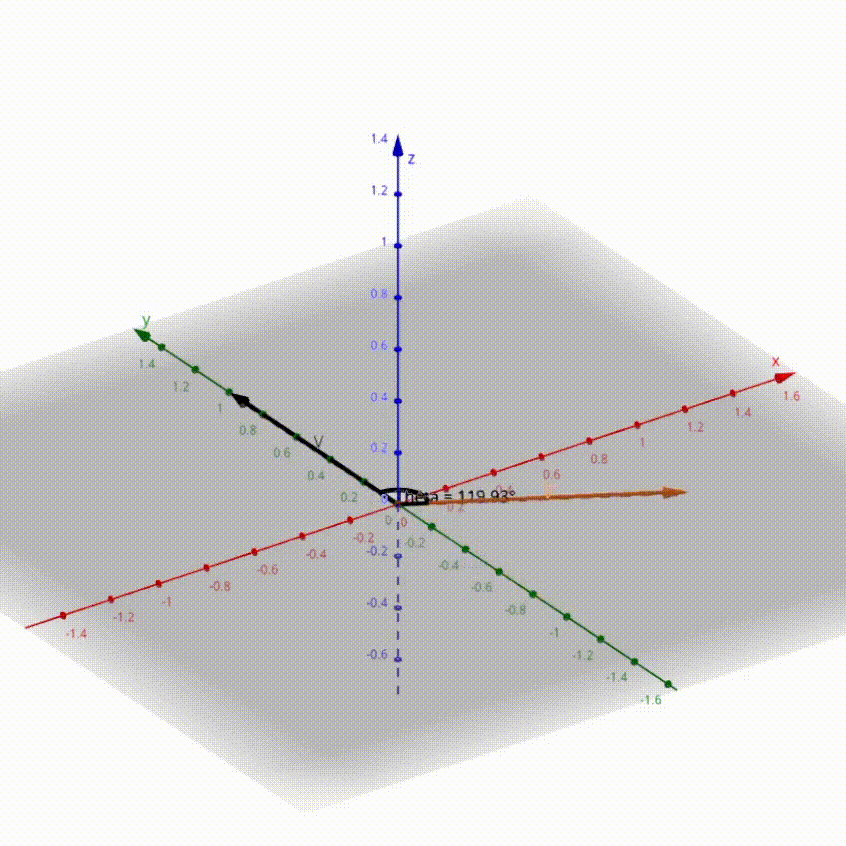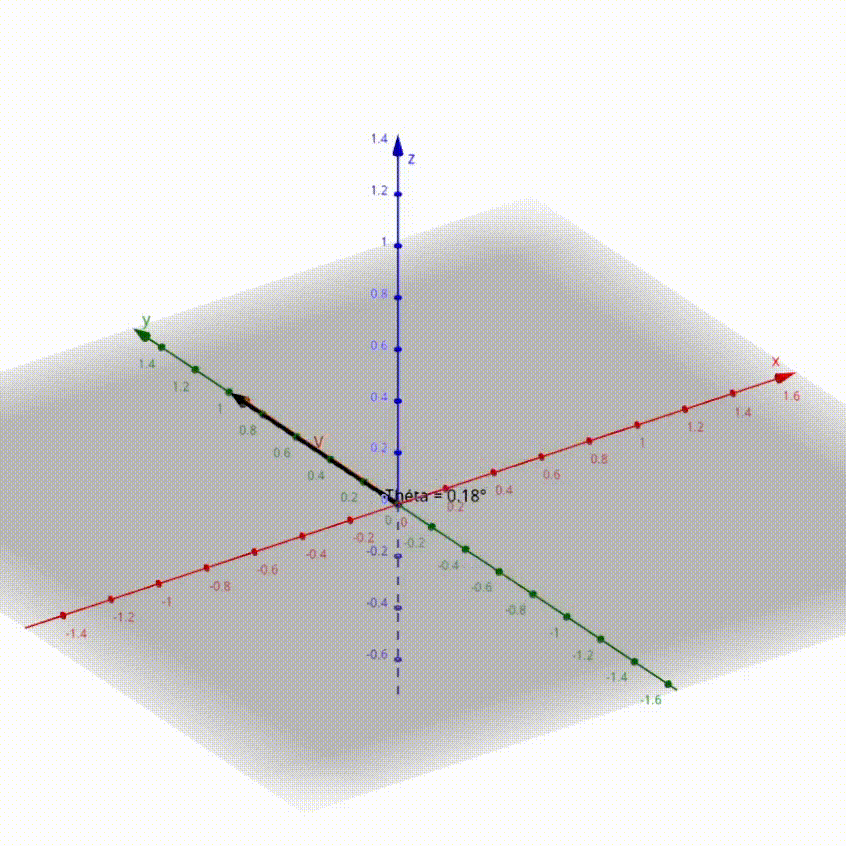Ici en noir le vecteur $V$ initial et en orange le vecteur $V'$ tourné de $\theta$_ Super ! On sait maintenant faire tourner notre référentiel caméra, il faut maintenant pouvoir exprimer nos points de l'espace dans ce référentiel. Rien de plus simple, on va utiliser la matrice de passage de la base $B_{cam}$ dans $B_c$ : $P_{B_{cam}, B_c}$ Par soucis de simplicité, on va d'abord exprimer $P_{B_c, B_{cam}}$ qui revient à écrire les coordonnes de nos vecteurs $v_1,v_2,v_3$ dans la base canonique. En notant $v_i = (x_i, y_i, z_i), i\in\{1, 2, 3\}$, on a $$ P_{B_c, B_{cam}} = \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \\ \end{pmatrix} $$ En remarquant que $B_{cam}$ et $B_c$ sont des bases orthonormées, $P_{B_{cam}, B_c}$ = $(P_{B_c, B_{cam}})^T$ Il ne reste plus qu'à exprimer nos points formant nos triangles dans la base de notre caméra par la relation : $$\begin{pmatrix} x' \\ y' \\ z' \\ \end{pmatrix} = P_{B_{cam}, B_c} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix}$$ avec $\begin{pmatrix} x \\ y \\ z \\ \end{pmatrix}$ les coordonnées d'un point quelconque de $\mathbb{R^3}$. --- Nous avons fini toutes les maths dont nous avions besoin, ou presque. Maintenant que l'on a tous nos points écrits dans la base de la caméra, il nous suffit alors de faire le rendu. Pour faire le rendu, en plus de changer de base, il faut ramener le triangle aussi proche de l'origine qu'il l'est de la caméra. On aura donc tous nos calculs faits depuis l'origine, ce qui les allège. On utilisera, pour le moment, la méthode décrite [ici](https://en.wikipedia.org/wiki/3D_projection#Diagram) (où la distance focale est égale à 1) pour projeter nos points sur un plan 2D. Elle nous sera suffisante pour l'instant pour donner l'illusion de distance et de 3D. ```C vec2 projection_to_2D(vec3 v){ if (v.y < EPSILON && v.y > - EPSILON) return UNDEFINED_VEC2; vec2 res = {v.x/v.y, v.z/v.y}; return res; } ``` _Ici, on renvoie un vecteur indéfini si on veut diviser par 0, la comparaison à un epsilon petit (=0.0001) nous est amplement suffisante pour notre utilisation vu qu'on ne peut comparer réellement des flottants._ Plus qu'à appliquer les fonctions de normalisation sur l'écran et d'affichage et **la magie opère !** ```C for(int i = 0; i < n; i++){ triangle3D t = changeReferenceToCamera(cam, objects[i]); t.v1 = sub_vec3(t.v1, cam->pos); t.v2 = sub_vec3(t.v2, cam->pos); t.v3 = sub_vec3(t.v3, cam->pos); // Vérifie que le triangle est bien devant la caméra if (t.v1.y <= 0 || t.v2.y <= 0 || t.v3.y <= 0) continue; triangle2D t2 = project_triangle3D_to_2D(t); draw_triangle2D(screen, triangle2D_to_screen(screen, t2)); } ``` _On note la condition qui nous sort de la boucle si le triangle n'est pas censé être affiché, et les deux dernières fonctions qui nous permettent d'abord d'obtenir un triangle aux coordonnées normalisées `triangle2D_to_screen()` (entre -1 et 1) et `draw_triangle2D()` qui, elle, affiche les caractères formant "l'intérieur" du triangle, comme fait dans le début de la série de vidéos mentionnée au début._  _Le résultat final !_